In un precedente articolo abbiamo visto che le grotte si comportano come le casse di risonanza degli strumenti musicali. In particolare, abbiamo descritto il caso semplificato di una grotta con un ampio salone di lunghezza, profondità e larghezza più o meno uguali tra loro e connesso con l’esterno da uno o più pozzi. Quando un’onda di pressione entra nel salone scuote le molecole d’aria, che sono libere di muoversi finchè non incontrano una parete. Le pareti riflettono l’onda facendola interferire con le oscillazioni già presenti nella sala. Quando la lunghezza d’onda della perturbazione è tale da adattarsi alla geometria della grotta, l’onda di pressione viene amplificata: la grotta entra in risonanza e le oscillazioni dell’aria raggiungono la massima ampiezza. La frequenza naturale di risonanza dipende inversamente dal volume della sala: grotte grandi suonano con toni gravi (frequenze basse) e viceversa grotte piccole risuonano con toni acuti (frequenze alte). Il fatto che la frequenza naturale dipenda solo dal volume e non dalla forma è vero solo sotto l’ipotesi che la sala sia approssimabile a una sfera, ovvero che l’onda venga riflessa nello stesso modo lungo qualunque direzione.
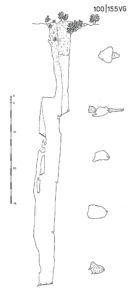
Cosa succede quando la forma della grotta non è semplicemente un grande vuoto sferico? Come si può intuire, la grotta avrà ancora una frequenza naturale ma essa dipenderà esplicitamente dalla forma e dalle dimensioni della cavità. Se potessimo trovare questa relazione per grotte arbitrariamente complesse, saremmo in grado di dedurre la forma di una cavità semplicemente ascoltando le sue frequenze di risonanza. In generale questo è un compito difficilissimo ma in casi estremamente semplificati è possibile trovare questa relazione e trarne alcune utili conclusioni. Nel seguito ci occuperemo delle grotte a pozzo o a galleria.
Sul Carso si incontrano frequentemente pozzi di varie profondità e dimensioni. La maggior parte sono brevi pozzi profondi al massimo qualche decina di metri, alcuni invece superano i 100 metri di profondità. Più raramente possiamo visitare gallerie naturali o artificiali a fondo cieco, o ancora tunnel naturali che forano da parte a parte una collina. Ciascuno di questi esempi rappresenta una grotta approssimabile ad un tubo, poiché una delle dimensioni (la lunghezza) è sensibilmente più grande delle altre due. Queste grotte hanno una geometria semplice ma non per questo poco interessante. Grazie alla loro forma allungata, in condizioni non turbolente l’aria si muoverà quasi esclusivamente nel senso della lunghezza, oscillando avanti e indietro lungo l’asse della grotta. Dunque, possiamo aspettarci che la loro frequenza naturale dipenda principalmente dalla lunghezza della grotta. Divideremo le grotte a tubo in due categorie: grotte a due ingressi e grotte a un ingresso, ovvero a fondo cieco.
Il comportamento delle grotte a tubo è analogo a quello di strumenti a fiato come il flauto dolce, il flauto traverso, il clarinetto, e l’organo. Anche questi strumenti sono dei tubi rettilinei, e presentano delle aperture alle estremità. Anch’essi risuonano quando un’onda di pressione li attraversa. Per rendere più calzante l’analogia, supporremo di tenere chiusi tutti i fori intermedi che normalmente consentono di suonare note di altezza diversa. Nonostante il clarinetto e il flauto possano sembrare simili a parte le loro dimensioni, in realtà funzionano in modo alquanto diverso: il primo corrisponde a una grotta a due ingressi, il secondo a una grotta a fondo cieco.
Il funzionamento del flauto dolce e le grotte a due ingressi
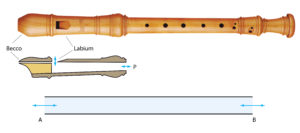
La figura a lato mostra un flauto dolce e la sua sezione longitudinale. Il flautista soffia nel becco dello strumento. Il getto d’aria viene spinto contro una scanalatura affilata chiamata labium, senza la quale il flauto non funzionerebbe. Quando il getto d’aria incontra il labium, ne viene deviato. Questo provoca una momentanea diminuzione della pressione all’interno del flauto, che richiama aria dalla scanalatura. L’aria richiamata crea una sovrapressione che spinge nuovamente il getto all’esterno. Il ciclo si ripete creando una pulsazione della pressione che si propaga nello strumento. Soffiando con la giusta intensità, lo strumento risuona. Lo scopo del becco è solo quello di dirigere il soffio verso il labium e non costituisce un foro ai fini della produzione del suono. Siccome la bocca del musicista poggia sul becco, quel foro è chiuso a tutti gli effetti e quindi il flatuo dolce non è altro che un tubo aperto su entrambe le estremità. Possiamo pensarlo come una grotta a due ingressi. Anche il flauto traverso è un tubo aperto: questa volta il foro su cui si soffia funge contemporaneamente da becco e da labium. Il trucco è soffiare radente alla cosiddetta boccola (su cui si appoggiano le labbra) in modo che il getto d’aria venga separato dallo spigolo opposto della boccola stessa. Allo stesso modo, una grotta può essere suonata da un vento radente all’ingresso.
Il funzionamento del clarinetto e le grotte a un ingresso

Il funzionamento di un clarinetto è alquanto diverso dal flauto dolce. Sul clarinetto non esiste il labium, ci sono solo il bocchino e il foro terminale. Come viene prodotta l’oscillazione in assenza del labium? Il problema viene risolto dall’ancia, una lamina di legno sottile fissata al bocchino. La pressione dell’aria nella bocca del clarinettista, maggiore della pressione atmosferica, mette in vibrazione l’ancia la quale immette alternativamente aria in sovra- e sotto- pressione nella canna del clarinetto. Le ance sono tarate in modo da stimolare una risonanza nello strumento. Anche in questo caso il bocchino è occluso dunque l’aria ha solo il foro terminale dello strumento per vibrare liberamente. A tutti gli effetti, possiamo schematizzare il clarinetto come un tubo con un lato aperto e uno chiuso. Dunque, è analogo ad una grotta a fondo cieco con un ingresso. Nelle grotte non c’è un’ancia, ciononostante le oscillazioni della pressione esterna possono mettere in risonanza una grotta a fondo cieco come se fosse un clarinetto.
Suono delle grotte a due ingressi
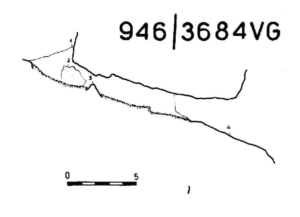
Entreremo ora nel dettaglio e vedremo come risuona una grotta a due ingressi, ovvero un tubo con due aperture. Questo caso si applica ad esempio a una galleria che fori da parte a parte una collina. Come abbiamo visto nell’esempio dell’altalena in un precedente articolo, il fenomeno della risonanza ha una peculiarità: una volta trovata la giusta frequenza, basta una piccolissima spinta per ottenere un’ampia oscillazione dell’altalena. Se portiamo questo esempio all’estremo, ne concludiamo che – a patto di lavorare esattamete a risonanza – possiamo addirittura rimuovere lo stimolo esterno e, in assenza di dissipazione, l’altalena continuerà ad oscillare autonomamente. Lo stesso vale per le onde di pressione in una grotta a due ingressi. Supponiamo che una pertubazione atmosferica faccia oscillare l’aria all’interno della grotta. Una volta innescata la risonanza, basta una piccolisima deviazione dalla pressione esterna per sostenere l’onda all’interno della grotta. Ne deduciamo che in ciascun ingresso la pressione non oscilla, o comunque si mantiene vicinissima a 1 atm. Questo non significa che nella grotta nulla si muova: al contrario!
Le onde di pressione sono deviazioni in positivo o in negativo dal valore medio. Rappresenteremo il valore della pressione in un punto \(x\) e in un istante \(t\) con \(p(x,t)\) e l’onda di pressione con \[\delta p(x,t)=p(x,t)-p_0\] dove \(p_0=1atm\). Per una grotta di lunghezza \(L\), chiamiamo i due ingressi \(x=0\) ed \(x=L\). Per quanto detto sopra, a risonanza la pressione ai due ingressi è pari alla pressione atmosferica. Se misurassimo la pressione in questi due punti, troveremmo sempre \(\delta p(0,t)=0\) e \(\delta p(L,t)=0\). Cosa accade nel frattempo dentro la grotta? Come l’altalena che va avanti e indietro alternativamente passando per il punto di equlibrio, la pressione interna oscilla in ogni punto della grotta: se ci sedessimo in un punto della galleria e misurassimo la pressione, troveremmo che oscilla regolarmente nel tempo. L’ampiezza di questa oscillazione dipende dal punto in cui misuriamo, ed è zero agli ingressi. Aggiungiamo infine un ultimo ingrediente: l’aria si sposta dalle zone di alta pressione a quelle di pressione inferiore. Per fare un esempio, se la pressione alla nostra sinitra è più alta che alla nostra destra, l’aria fluirà da sinistra a destra. Questa semplice osservazione ci consente di trovare tutte le onde di pressione compatibili con la grotta. Poniamoci all’ingresso di sinistra (\(x=0\)). Abbiamo detto che all’ingresso la pressione è di 1 atmosfera. Supponiamo che a 1 metro dentro la grotta ad un certo istante la pressione sia più bassa: 0.99 atm. L’aria verrà spinta verso il centro della grotta. Se la pressione calasse progressivamente fino all’ingresso di destra, l’aria uscirebbe dall’altra parte. Ma ciò non può succedere, perché al secondo ingresso (\(x=L\)) la pressione deve tornare ad 1 atmosfera. Dunque concludiamo che come la pressione cala allontanandoci dal primo ingresso, allo stesso modo deve risalire verso 1 atm al secondo ingresso. Siccome non c’è un trasporto netto d’aria da un ingresso all’altro, il profilo deve essere simmetrico, ovvero il massimo della sotto-pressione si trova al centro della grotta. Dopo un po’ di tempo, questa sottopressione richiamerà aria e il ciclo si invertirà. Gradualmente la pressione tornerà a 1 atmosfera, e aumenterà finché l’aria non sarà compressa al centro della grotta. A questo punto il ciclo ricomincia. Ne concludiamo che i due ingressi aspirano o soffiano contemporaneamente. Questo profilo corrisponde alla nota più grave che la grotta possa contenere: abbiamo trovato l’armonica fondamentale. Se facciamo un grafico della pressione misurata nei vari punti della grotta in un istante di tempo generico, troviamo il seguente grafico:
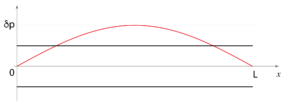
I punti in cui la pressione si annulla si chiamano nodi. Sono punti speciali perché lo scostamento dalla pressione atmosferica rimane a zero per tutto il tempo. Dal grafico riportato sopra, notiamo un fatto interessante: la grotta contiene solo mezza lunghezza d’onda della curva rossa. Dunque la lunghezza d’onda dell’armonica fondamentale è \(\lambda=2L\). Questo fatto diventa più chiaro se lo visualizziamo in un grafico. L’onda acustica ha una lunghezza d’onda pari al doppio della lunghezza della grotta: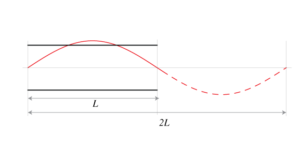
Da queste informazioni possiamo trovare il valore della frequenza fondamentale. Ricordiamo che la velocità del suono è il prodotto della frequenza per la lunghezza d’onda: \(c=f\lambda\) (\(c\simeq 343m/s\)). Dunque, l’armonica fondamentale ha una frequenza pari a \[f_1=\frac{c}{2L} \quad.\]
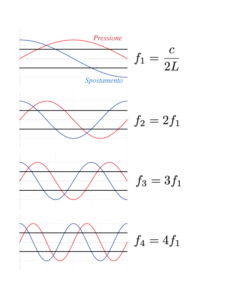 Grazie alla frequenza fondamentale, possiamo trovare tutte le armoniche possibili in una grotta di lunghezza fissata. Basta disegnare tutte le curve che hanno un nodo su entrambi gli ingressi (v. figura a lato). Ad esempio, possiamo aggiungere un nodo in mezzo alla grotta: basterà disegnare il profilo dell’armonica fondamentale in metà grotta e lo stesso profilo invertito nella seconda metà della grotta. Ora la grotta ospita esattamente una lunghezza d’onda (\(\lambda=L\)). La sua frequenza è il doppio della fondamentale \(f_2=c/L=2f_1\). Ripetendo questa costruzione possiamo aggiungere un altro nodo dividendo quindi la grotta in 3. La lunghezza d’onda è ora \(2/3L\) e la sua frequenza è \(f_3=3c/2L\). Continuando in questo modo troviamo tutte le armoniche di una grotta a due ingressi: \[f_n=\frac{c}{2L}n \quad,\quad n=1,2,3,4…\]
Grazie alla frequenza fondamentale, possiamo trovare tutte le armoniche possibili in una grotta di lunghezza fissata. Basta disegnare tutte le curve che hanno un nodo su entrambi gli ingressi (v. figura a lato). Ad esempio, possiamo aggiungere un nodo in mezzo alla grotta: basterà disegnare il profilo dell’armonica fondamentale in metà grotta e lo stesso profilo invertito nella seconda metà della grotta. Ora la grotta ospita esattamente una lunghezza d’onda (\(\lambda=L\)). La sua frequenza è il doppio della fondamentale \(f_2=c/L=2f_1\). Ripetendo questa costruzione possiamo aggiungere un altro nodo dividendo quindi la grotta in 3. La lunghezza d’onda è ora \(2/3L\) e la sua frequenza è \(f_3=3c/2L\). Continuando in questo modo troviamo tutte le armoniche di una grotta a due ingressi: \[f_n=\frac{c}{2L}n \quad,\quad n=1,2,3,4…\]
Abbiamo raggiunto un risultato interessante: una grotta a due ingressi risuona con tutti i multipli interi della frequenza fondamentale. Vedremo che la situazione è diversa per grotte a fondo cieco.
Ora che consociamo il comportamento della pressione, possiamo dedurre il movimento dell’aria. Se in una regione la pressione varia bruscamente, lo spostamento d’aria sarà maggiore. La massima varizione di pressione si trova ai nodi, dunque lo spostamento d’aria è massimo in questi punti (in particolare agli ingressi). Ne ricaviamo la seguente regola. Ai nodi della pressione corrispondono i picchi dello spostamento, e ai picchi della pressione corrispondono i nodi dello spostamento.
Le seguenti animazioni mostrano un’onda di pressione (in rosso) e il corrispondente spostamento d’aria (in blu). I punti neri rappresentano le molecole d’aria.

Notiamo inoltre che il verso dello spostamento è uguale al gradiente di pressione. Nelle armoniche dispari (1,3,…) i gradienti di pressione agli ingressi sono opposti e di conseguenza entrambi gli ingressi soffiano (o aspirano) contemporaneamente. Viceversa, nelle armoniche pari (2,4,…) il gradiente di pressione ha lo stesso segno ai due ingressi quindi la colonna d’aria aspirata da un ingresso viene espulsa dall’altro.
Suono delle grotte a un ingresso
Quando la grotta ha un fondo cieco, le frequenze di risonanza cambiano. Per analizzare questa geometria, è più semplice ragionare in termini dello spostamento d’aria. Chiameremo \(x=0\) il fondo e \(x=L\) l’ingresso. La parete di fondo blocca lo spostamento d’aria, e infatti le molecole a contatto con la parete non possono muoversi. Dunque lo spostamento d’aria ha un nodo sulla parete di fondo. Di conseguenza, la pressione deve raggiungere un picco sulla stessa parete. D’altra parte, l’ingresso si comporta esattamente come abbiamo visto in precedenza: la pressione è pari alla pressione atmosferica, dunque \(p(L,t)=0\). Riassumendo, in una grotta a fondo cieco la pressione ha un nodo all’ingresso e un picco sulla parete di fondo:
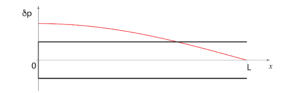
La massima lunghezza d’onda che risponde a questi requisiti è quattro volte la lunghezza della grotta, come indicato nella figura seguente:
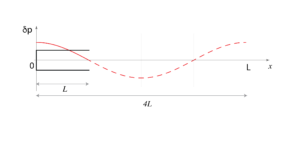
La frequenza fondamentale sarà quindi \[f_0=\frac{c}{4L} \quad.\] Se confrontiamo questo risultato con quello ottenuto in precedenza, troviamo che una grotta a due ingressi risuona con una nota fondamentale più acuta di una grotta a fondo cieco della stessa lunghezza. Per la stessa ragione, un clarinetto ha un suono più grave di un flauto dolce o traverso della stessa lunghezza.
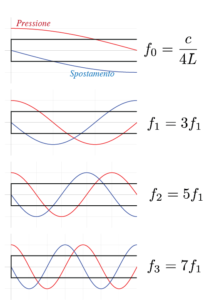
Seguendo lo stesso ragionamento visto in precedenza, possiamo trovare tutte le armoniche superiori inserendo un numero intero di profili fondamentali all’interno della grotta. Tuttavia, c’è un’importante differenza. Suponiamo di dividere la grotta in due, e di inserire 1/4 di lunghezza d’onda tra l’ingresso e il centro, e la sua immagine riflessa tra il centro e il fondo. C’è un problema: l’onda ottenuta ha un nodo anche sulla parete di fondo, mentre dovrebbe avere un picco. Quindi non possiamo inserire un multiplo pari dell’onda fondamentale. La parete di fondo elimina tutte le armoniche pari, dunque concludiamo che per questo tipo di grotte tutte le frequenze di risonanza sono multipli dispari della frequenza fondamentale: \[f_n=\frac{c}{4L}(2n+1) \quad,\quad n=0,1,2,3,…\]
In conclusione, se tutte le armoniche misurate sono mutlipli dispari della frequenza fondamentale, significa che la grotta ha un fondo occluso. Le seguenti animazioni mostrano lo spostamento della colonna d’aria all’interno della grotta. Come previsto, lo spostamento è nullo sul fondo. Le stesse animazioni, ruotate di 90 gradi, illustrano la propagazione dell’aria in un pozzo verticale.

Per avere un’idea delle frequenze tipiche delle grotte, facciamo un esempio: un abisso di 100 metri ha una frequenza di risonanza fondamentale pari a \[f_1=\frac{343m/s}{4\times 100m}\simeq 0.86 \,Hz \quad,\] ovvero una oscillazione ogni 1.17 secondi circa. Passaggi di perturbazioni, turbolenze dell’atmosfera o effetti dovuti al vento possono facilmente attivare queste frequenze di risonanza.
Bibliografia
[1] Wolfe, J., Open vs Closed pipes (Flutes vs Clarinets) [webpage]
[2] Pierce, A. D., Acoustics – An Introduction to Its Physical Principles and Applications, 3rd edition. Springer (2019)



