
L’aria nelle Grotte
Quando pensiamo alle grotte immaginiamo pareti rocciose, frane, speleotemi, cristalli. A questa componente solida corrisponde specularmente la parte aerea delle grotte. Una grotta è un vuoto, dunque è principalmente una regione di spazio che non contiene roccia. Questo vuoto è occupato dall’aria e dai suoi movimenti.
Essendo un fluido, l’aria si muove e circola all’interno delle montagne, trasportando con sé l’energia che ha accumulato all’esterno e depositandola in grotta contribuendo indirettamente a creare una ricchissima varietà di fenomeni e morfologie. Quando riemerge in superficie, l’aria contiene in sé un’impronta della grotta che ha attraversato. La possiamo paragonare a un messaggero che trasporta incessantemente informazioni tra l’interno e l’esterno. L’energia dell’aria è tra i principali motori che scolpiscono e modellano l’ambiente sotterraneo, assieme a quella trasportata dall’acqua, quella accumulata nella tensione della roccia e quella scambiata nelle reazioni chimiche e bio-chimiche. L’aria ha una caratteristica speciale rispetto alle altre componenti: agisce velocemente su grandi distanze. Ad esempio, il passaggio di un temporale innesca onde di pressione che in breve tempo raggiungono, pur attenuate nella loro ampiezza, tutti i vani della grotta. Grazie alla sua mobilità, l’aria redistribuisce velocemente la sua energia all’interno delle grotte. In condizioni normali né l’acqua, né la roccia, né i processi chimici agiscono così rapidamente a lungo raggio.
Così come i pesci vivono perfettamente adattati alle profondità marine, gli speleologi si muovono immersi in un oceano d’aria, con le sue onde, le sue correnti e i suoi vortici. L’aria è particolarmente utile agli speleologi, non solo per respirare ma anche per esplorare. Seguire l’aria è la regola aurea dell’esploratore: un refolo inatteso può indicare la presenza di vani nascosti e sorprendenti prosecuzioni.
I prossimi paragrafi descrivono un fatto semplice ma dalle sorprendenti conseguenze: le grotte attraversate dall’aria risuonano come degli strumenti a fiato. Nello stesso modo in cui un clarinetto ha un timbro diverso da un fagotto, grotte di forma diversa risuonano in modo diverso. Registrando le oscillazioni dell’aria all’ingresso si può scoprire quanto sia grande il volume sottostante senza essere mai scesi in quella grotta. Di più: il suono prodotto all’ingresso dipende dalla forma stessa della grotta. Dunque, se si potesse “ascoltare” la forma delle grotte, i suoni e le voci delle grotte potrebbero guidare gli speleologi nelle esplorazioni.
Francesco Serafin, 25 Aprile 2022
LE GROTTE COME CASSE DI RISONANZA
Grotte e birre, si sa, sono indissolubilmente legate. Immaginiamo un gruppo di speleo al rientro da un’esplorazione, che si rinfresca con una cassa di birre lasciate al fresco in qualche freezer naturale. Già dopo un paio di sorsi, lo speleo ispirato può brandire la bottiglia, portarla alle labbra e soffiare radente all’imboccatura. Ecco che un suono abbastanza pulito e acuto si sprigiona dalla bottiglia, per la gioia della compagnìa. Per riprender fiato, dopo un po’ lo speleo beve altri due sorsi. A questo punto la bottiglia è vuota, urge sostituirla con una nuova, ma prima si ritenta l’assolo: stavolta il fischio è più basso. Inoltre si ottiene più o meno lo stesso suono da una qualunque delle bottiglie vuote della cassa.

Il soffio dello speleo produce un flusso d’aria più o meno caotico sul collo della bottiglia. Infatti, il soffio di per sé è un rumore indistinto, ovvero è un misto incoerente di molti suoni puri a frequenze e intensità diverse. Il punto fondamentale è che la perturbazione può essere caotica ma, a patto di usare una bottiglia simile, la frequenza del suono emesso è sempre la stessa e dipende solo da quanta aria c’è nella bottiglia. Questo significa che la bottiglia agisce da filtro selezionando automaticamente una nota pura da un miscuglio incoerente (il soffio).
Il fenomeno appena descritto è esattamente ciò che accade a una grotta quando si verifica una perturbazione nell’aria esterna. Una grotta ideale, ovvero sufficientemente semplice e liscia, con un solo ingresso, emette una nota (detta nota caratteristica) che dipende dal suo volume, esattamente come una bottiglia. Nella realtà le grotte hanno forme complicate, così che il suono emesso è più sporco di una nota pura. Ciononostante, la nota caratteristica domina sulle altre e la sua intensità sovrasta gli altri toni.
Come fanno una bottiglia o una grotta a selezionare proprio quella nota? E perché l’altezza della nota dipende dal volume d’aria contenuto nella bottiglia? Per capirlo, dobbiamo salire su un’altalena.
La Risonanza

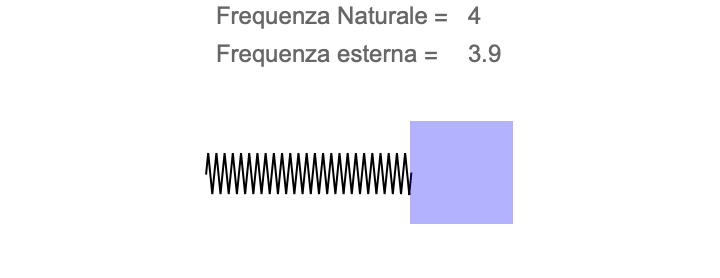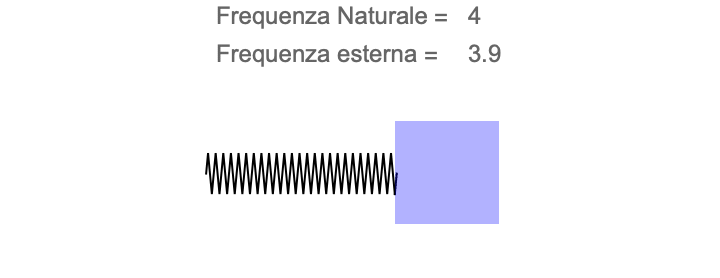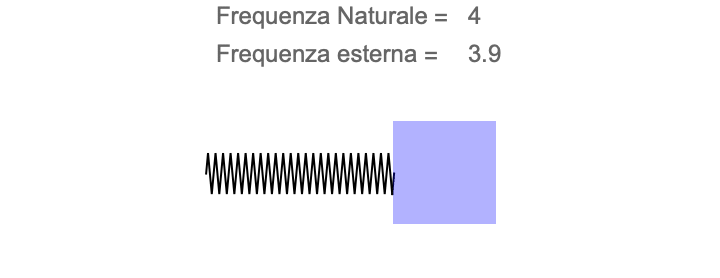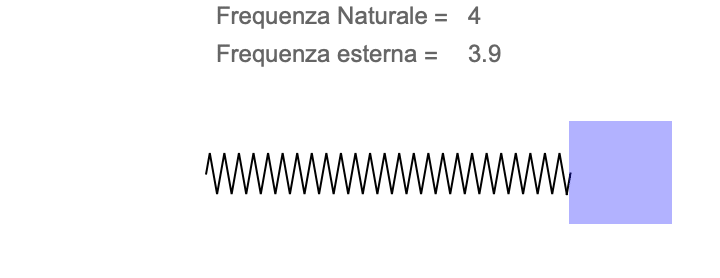
Quando ci sediamo sull’altalena e ci diamo una spinta, l’altalena comincia ad oscillare ad una frequenza ben precisa (almeno finché l’attrito non la smorza). La frequenza è la stessa, sia che spingiamo con forza sia che spingiamo poco. La frequenza dell’altalena è una sua caratteristica propria e dipende solo dalla lunghezza del cavo (e non dalla massa di chi ci sta sopra!). La chiameremo frequenza naturale dell’altalena.
Quando spingiamo qualcuno sull’altalena, sappiamo che dare spinte a caso non dà grandi risultati. Infatti, se spingiamo a ritmi sempre diversi, non facciamo altro che scuotere l’altalena a frequenze tutte diverse: esse si cancellano tra loro (come un’orchestra che suona a caso produce rumore incoerente) e l’altalena non “decolla”.

Se invece ci sincronizziamo con l’altalena, una piccola spinta applicata col giusto ritmo è in grado di spingere l’altalena sempre più in alto, con oscillazioni sempre più ampie. La sensazione è che l’altalena selezioni per noi la frequenza giusta alla quale deve essere spinta. E in effetti è proprio ciò che accade. Quando abbiamo trovato il ritmo giusto, significa che siamo in risonanza con la frequenza naturale dell’altalena. Ogni volta che l’altalena torna verso di noi, e riceve una nuova spinta, la nostra energia non viene dispersa tra tutte le possibili frequenze di oscillazione ma viene aggiunta di volta in volta all’oscillazione naturale, con l’effetto di aumentare sempre più l’ampiezza dell’oscillazione.
L’altalena, come ogni pendolo, funziona con un moto periodico. La sua condizione di equilibrio è quando il seggiolino è sulla verticale della fune. Se la lasciamo in questa posizione, ci rimarrà per sempre. Se la allontaniamo dalla posizione iniziale, oscillerà intorno all’equilibrio. A tutti gli effetti, possiamo immaginare che invece della gravità e della fune, ci sia una molla ancorata al punto di equilibrio, che costringe l’altalena a ripassare sempre attraverso di esso, indipendentemente da quanto lontano la tiriamo.
Per quanto bizzarro, l’altalena, la bottiglia e la grotta funzionano tutte con lo stesso meccanismo: la risonanza. Vediamo quindi come applicare l’esempio dell’altalena alla grotta.


Un’altalena fatta d’aria
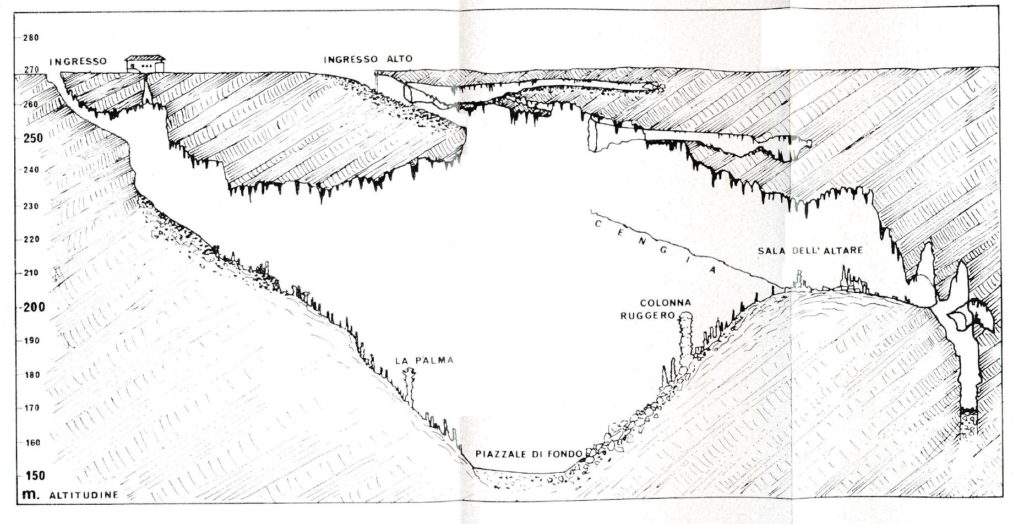
Immaginiamo una grotta molto semplice. Un ingresso di modeste dimensioni, un pozzo e sotto di esso una vasta caverna, contenente un grande volume d’aria. Variazioni di pressione dovute al passaggio di perturbazioni attivano circolazioni d’aria che alternativamente entrano ed escono dalla grotta. Queste grotte vengono dette cavità barometriche. La Grotta Gigante (se tappiamo l’ingresso turistico) ne è un classico esempio. Chiediamoci: esiste una frequenza naturale per questa grotta?
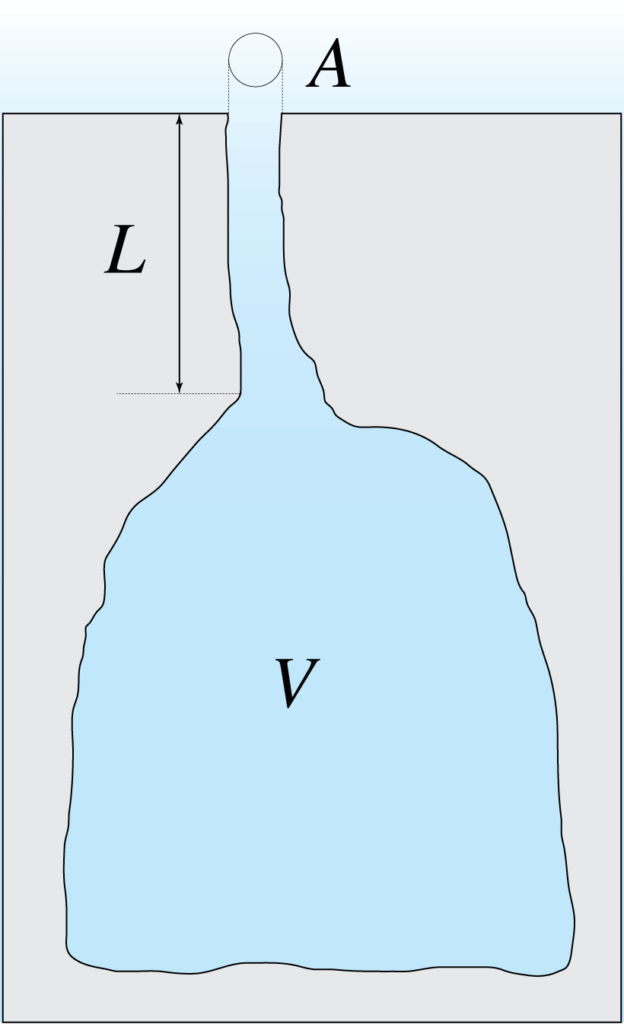
Cerchiamo un’analogia tra l’altalena e la grotta. A cosa corrisponde il seggiolino dell’altalena, e qual’è la molla che lo riporta verso l’equilibrio? Il seggiolino è l’aria contenuta nel pozzo d’ingresso. La molla è il grande volume d’aria sottostante. La condizione di equilibrio si ha quando l’aria è immobile in tutta la grotta.
Se spingiamo la colonna d’aria del pozzo verso la sala, il volume sottostante viene compresso e dunque reagisce con una pressione sul fondo della colonna. Questa è la molla. Rilasciando il pistone, l’aria del pozzo viene spinta nuovamente verso la posizione iniziale. Siccome sta accelerando, la colonna supera la posizione di equilibrio ed esce dall’ingresso. A questo punto nella grotta c’è meno aria di prima, creando una sotto-pressione. L’aria viene richiamata all’interno e il ciclo continua. Abbiamo realizzato un’altalena d’aria.
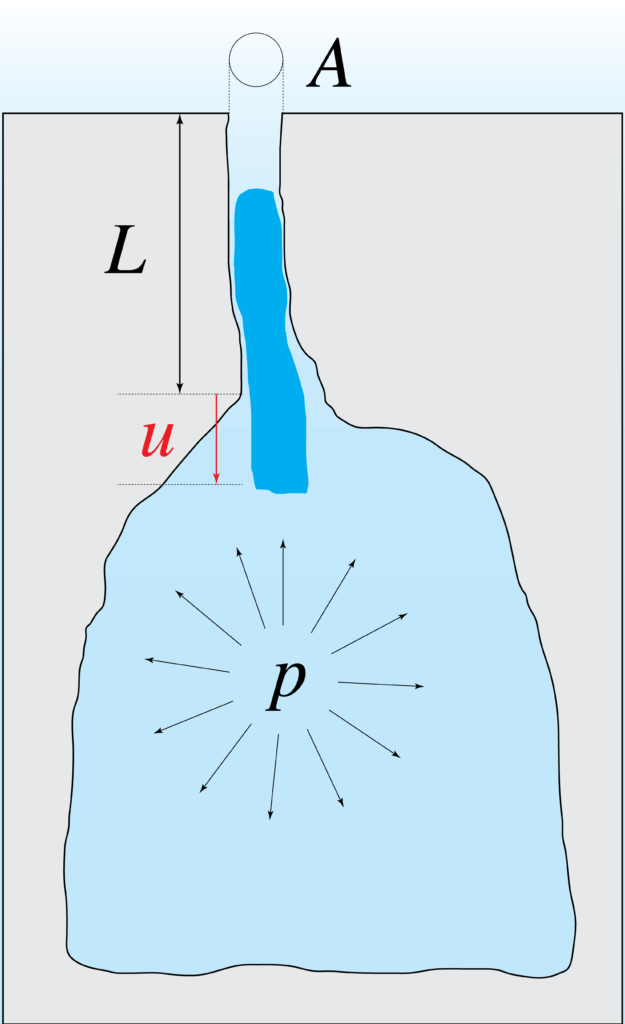
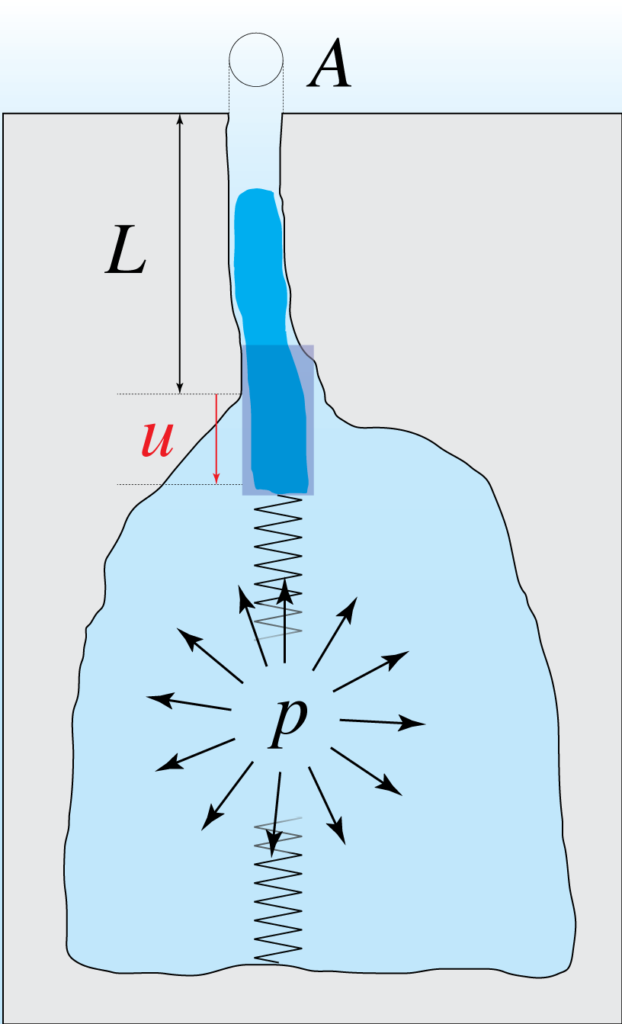
Quando una perturbazione o una turbolenza raggiunge l’ingresso di una grotta, muove la colonna d’aria all’ingresso, mette in moto l’altalena e la grotta risuona.
Qual è la frequenza naturale della grotta? Come ricavato nell’appendice, essa è data da
\[ f_\mathrm{H}=\frac{c}{2\pi}\sqrt{\frac{A}{VL}}\]

(fonte: Wikipedia)
La cosa importante è che dipende dalla geometria della grotta: \(A\) è l’area dell’ingresso, \(L\) è la lunghezza del pozzo, \(V\) è il volume della sala, e \(c=343\,m/s\) è la velocità del suono. Notiamo che se aumentiamo il volume della grotta, la frequenza scende: infatti ad esempio un contrabbasso emette suoni più gravi (bassa frequenza) di un violino (alta frequenza). Dunque grotte grandi emettono suoni più gravi.
Dunque, come l’altalena amplifica il suo moto quando riceve la spinta giusta, così una grotta risuona quando nella perturbazione esterna esiste una frequenza che è compatibile con la geometria della grotta.
Basandosi su questo fenomeno, a metà dell’Ottocento il fisico Hermann von Helmoltz costruì una piccola cavità in ottone e la usò per trovare le frequenze pure contenute nei rumori caotici che incontriamo quotidianamente, come il vento, lo scrosciare dell’acqua, o per analizzare i timbri degli strumenti musicali. Oggi questo strumento è noto come risuonatore di Helmoltz. Quando viene investito da un miscuglio di frequenze, il risuonatore le smorza tutte tranne la sua frequenza naturale, che viene amplificata dalla cavità fino a diventare udibile. Avvicinandolo all’orecchio, se la nota era presente nel segnale turbolento la sentiamo amplificata all’interno del risuonatore. Le conchiglie funzionano allo stesso modo. Anche gli strumenti musicali sono fatti da casse di risonanza (si pensi alle chitarre o ai violoncelli). Grazie alle loro forme selezionano alcune frequenze e le amplificano Ecco perché le grotte agiscono da filtri acustici.
Il respiro della Grotta Gigante
Possiamo stimare la frequenza naturale della Grotta Gigante conoscendo le sue misure. L’ingresso si può chiudere con una porta su cui è ritagliata una finestrella di area \(A=(0.3)*(0.4)\,m^2\). La lunghezza del pozzo è \(L=10\,m\) circa. Il volume stimato è \(V=350.000\,m^3 \, – \, 500.000\,m^3\). Dunque, la frequenza naturale \(f_\mathrm{Gigante}\) è compresa tra \(0.0085-0.01\, Hz\) (\(1Hz\) = 1 ciclo al secondo). Il suo reciproco ci dà un periodo di inversione dell’aria di \[T_\mathrm{Gigante}=98–118\, s\]Infatti, i valori misurati con i barometri di precisione all’ingresso mostrano una chiara oscillazione tra i 20 e i 100 secondi [1,2]. Il fatto che il valore predetto dal semplicissimo modello di risonanza si avvicini così tanto al valore osservato è sorprendente, se si pensa che il modello trascura tutti gli effetti di turbolenza dovuti alla rugosità delle pareti!
I suoni udibili hanno frequenze comprese tra i 20 e i 20.000 Hertz. Come abbiamo visto nel caso della Grotta Gigante, i suoni delle grotte hanno frequenze molto più basse, dai millesimi fino ai centesimi di Hertz. Vengono chiamati infrasuoni e non sono udibili dall’orecchio umano ma sono misurabili con barometri e anemometri che registrano gli spostamenti d’aria causati dalla risonanza.
Ricavare il volume di una grotta
La formula della frequenza naturale della grotta risulta utilissima anche se scritta al contrario: possiamo ricavare il volume di una grotta misurando l’area dell’ingresso, la profondità del pozzo di accesso, e la frequenza delle correnti d’aria (o della pressione) che escono dall’ingresso!
\[V=\frac{1}{4\pi^2}\frac{c^2}{ f_\mathrm{H}^2}\frac{A}{L}\]
Una grotta con molti ingressi
Cosa succede se una grotta ha molti ingressi? La grotta possiede ancora una frequenza naturale, l’unica differenza è che le colonne d’aria nei vari ingressi si muoveranno più o meno vigorosamente a seconda della sezione e della lunghezza del pozzo. Per ricavare la formula della frequenza naturale ci vuole un po’ di algebra, ma per fortuna il risultato ha un’espressione molto semplice.
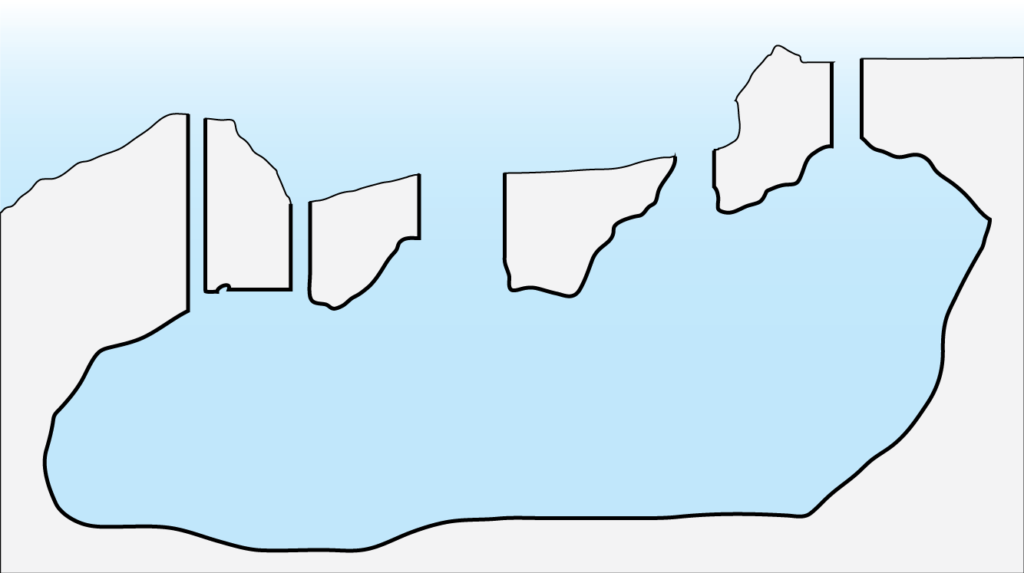
Ogni ingresso ha una sua sezione \(A_j\) e una sua lunghezza \(L_j\) dove \(j\) è il numero dell’ingresso. La frequenza naturale ora dipende dalla somma di tutte i rapporti \(A_j/L_j\) degli \(N\) ingressi: \[f_\mathrm{H}=\frac{c}{2\pi}\sqrt{\frac{1}{V}\sum_{j=1}^N\frac{A_j}{L_j}}\]
Quando la porta della Grotta Gigante viene aperta, la grotta ha due ingressi. I due pozzi hanno circa la stessa lunghezza, tra i 10 e i 12 metri. Il primo ha un’area di circa \(6m^2\) e il vano della porta nel secondo ha un’area di \(2m^2\). Usando i valori \(A_1/L_1=0.6m\) \(A_2/L_2=0.17m\) nella formula della frequenza di una grotta con due ingressi, otteniamo una frequenza \(f\sim0.068Hz\) ovvero un periodo di oscillazione della pressione di circa 15 secondi. Questo valore è in linea con le frequenze più alte misurate da S. Polli nella Grotta Gigante [2].
Quanto conta la forma del pozzo d’accesso?
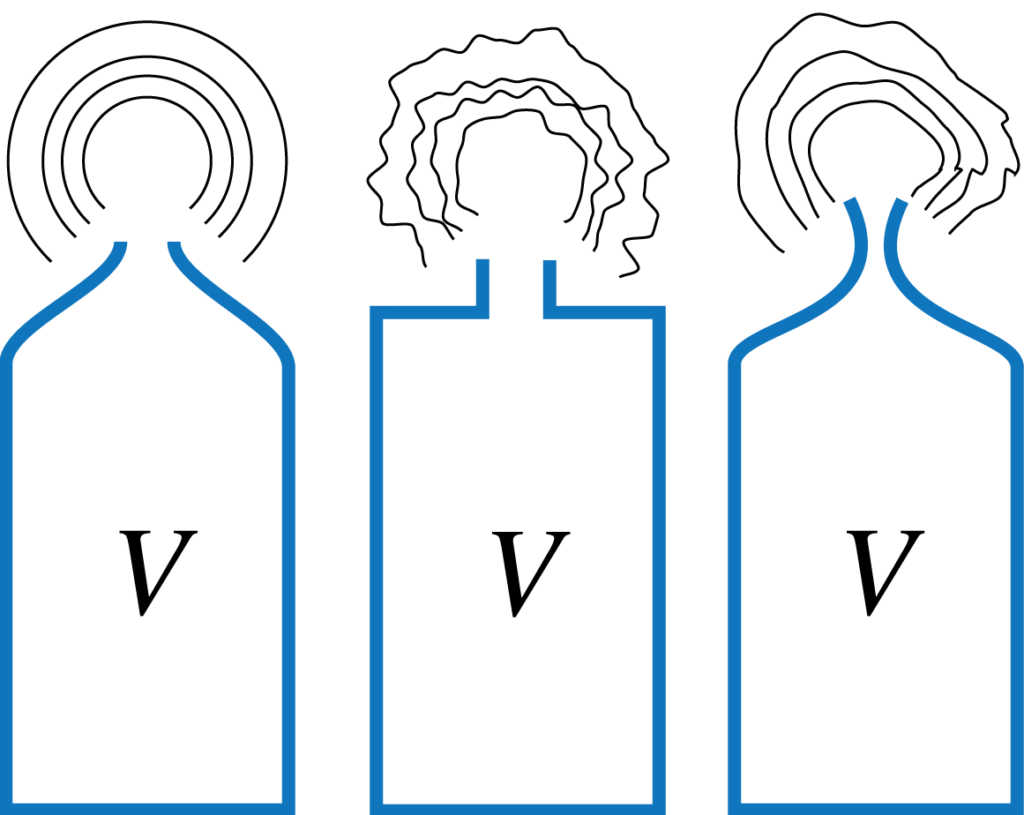
Le formule precedenti sono state ricavate sotto l’ipotesi che il pozzo d’accesso sia abbastanza corto rispetto al salone sottostante. In tal modo possiamo ignorare la reale geometria del pozzo approssimandolo ad un semplice cilindro. Questa semplificazione consente anche di supporre che le onde di pressione siano distribuite uniformemente nella cavità semplificando notevolmente il problema.
Nella realtà, la forma delle pareti può essere complessa. Le asperità riflettono il suono rendondolo meno uniforme. Si pensi ad esempio al flusso dell’acqua in un tubo di gomma: se il tubo è cilindrico l’acqua scorre uniformemente senza vortici, ma se stringiamo leggermente il tubo si formano vortici a monte e a valle del restringimento. Le turbolenze nel pozzo d’accesso fanno vibrare l’aria sovrapponendosi all’effetto altalena descritto in precedenza e quindi contribuiscono anch’esse a fissare la frequenza naturale della grotta. Quest’ultima non sarà più esattamente uguale alla semplice formula di Helmoltz, ma dovremo includere delle correzioni che dipendono dalla forma delle pareti. In generale questo è un problema complesso, poiché si tratta di immaginare come le onde acustiche seguano la forma della cavità.
BIBLIOGRAFIA
[1] Lewis, Warren C. Atmospheric Pressure Changes and Cave Airflow: A Review. NSS Bulletin 53 (1991)
[2] Polli, S. La grotta Gigante del Carso come cavità barometrica. Isitituto Sperimentale Talassografico Trieste 328 (1956), riprodotto in Atti e Memorie della Commissione Grotte E. Boegan 22, 235-262 (1983)
Appendice matematica
In questa appendice ricaviamo la frequenza naturale di una grotta.
Assumiamo che la dimensione massima della sala sia più piccola della lunghezza d’onda di risonanza. In questo modo la pressione all’interno della sala rimane uniforme.
Quando cerchiamo di schiacciare una bottiglia piena d’aria e tappata ermeticamente, sappiamo che incontriamo una certa resistenza. Ad una diminuzione del volume l’aria reagisce opponendo un aumento della pressione. Se il processo è rapido, non c’è il tempo per scambiare calore tra i vari punti del volume d’aria, quindi il processo avviene a temperatura costante. La rigidità dell’aria, proprio come la durezza di un pezzo di gomma, è data dal cosiddetto modulo di compressibilità \(K\). Esso misura quanto violenta sia la pressione generata \(\Delta P\) se il volume subisce una variazione relativa \(\Delta V/V\) (ad esempio, se vien compresso del 10%, \(\Delta V/V=0.1\). Secondo questa definizione abbiamo \[K=-\frac{\Delta P}{\Delta V/V} \quad.\] Per una compressione fissata, se \(K\) aumenta, la pressione generata sarà maggiore.
A questo punto, se l’aria viene compressa, reagirà sprigionando una pressione: \[\Delta P=-\frac{K}{V}\Delta V\]
La variazione assoluta del volume è data dallo spazio invaso dalla colonna d’aria quando penetra nella sala. Se la colonna scende di una quantità \(u\) (ad esempio, \(u=10m\)) il volume sottostante verrà schiacciato di una quantità \[\Delta V=-Au \quad.\] La variazione è negativa perché abbiamo supposto che il volume venga compresso. Mettendo tutto insieme: \[\Delta P= \frac{K}{V}Au\]
Il prossimo ingrediente è ricordare che il modulo di compressibilità è legato alla velocità di propagazione delle onde acustiche. Se percuotiamo un mezzo rigido (incomprimibile: \(K\) grande), il suono si propagherà velocemente all’interno di esso. Se percuotiamo un mezzo morbido (comprimibile: \(K\) piccolo), il suono si propagherà più lentamente. Esiste una relazione tra la densità \(\rho\) del mezzo (l’aria) la velocità del suono \(c\) e il modulo di compressibilità: \[K=\rho c^2\]
Mettendo insieme le due cose otteniamo \[\Delta P= \frac{\rho c^2}{V}Au \quad.\]
Dalla pressione, conoscendo l’area \(A\) del pozzo, è facile ricavarci la forza con cui il volume spinge sulla colonna d’aria: \[\Delta F=-\Delta P \cdot A= -\frac{\rho c^2A^2}{V}u\]
La forza è opposta allo spostamento, dunque c’è un segno meno. Infine, questa forza tenderà ad accelerare la massa della colonna d’aria, cercando di spingerla indietro, verso la posizione di equilibrio. La colonna d’aria ha una massa pari alla sua densità moltiplicata per il volume del pozzo, che per semplicità approssimiamo ad un cilindro di lunghezza \(L\) e sezione \(A\): \[m=\rho AL\]
Ora, l’ultimo passaggio. La forza dovuta alla compressione accelera la colonna d’aria secondo la legge di Newton: \(F=ma\) e l’accelerazione è la derivata seconda dello spostamento \(u\) rispetto al tempo, che indichiamo con \(\ddot{u}\). Usando i risultati trovati nelle due righe precedenti, troviamo l’espressione che lega l’accelerazione alla forza \[(\rho AL)\ddot{u}=-\frac{\rho c^2A^2}{V} \cdot u\]Dunque, abbiamo trovato che l’aria nella grotta si comporta come un oscillatore armonico di massa \(m=\rho AL\) e di costante elastica \(k=\rho c^2 A^2/V\). Sappiamo che la pulsazione naturale \(\omega\) di un oscillatore è il rapporto tra la rigidità della molla e la massa che viene accelerata. Dunque,
\[\omega=\sqrt{\frac{k}{m}}=c\sqrt{\frac{A}{VL}}\]
Infine, per trovare la frequenza dividiamo la pulsazione per \(2\pi\) e otteniamo
\[f_\mathrm{H}=\frac{c}{2\pi}\sqrt{\frac{A}{VL}} \quad.\]
Grotta barometrica con due ingressi (Avvertenza: contiene molta Algebra!)
Se abbiamo due ingressi, le cose si complicano. Adesso abbiamo due altalene, che comunicano tra di loro attraverso il volume \(V\). Diciamo che i pozzi 1 e 2 abbiano area e lunghezza \(A_1,L_1\) e \(A_2,L_2\). Gli spostamenti delle due colonne verranno indicati con \(u_1\) e \(u_2\). Quando le colonne d’aria si muovono, spostano i volumi \[\Delta V_1=A_1u_1 \quad \mathrm{e}\quad \Delta V_2=A_2u_2\]
La variazione totale del volume nella sala è quindi la somma dei due volumi spostati: \[\Delta V=-(\Delta V_1+\Delta V_2)=-A_1u_1-A_2u_2\]
Il movimento delle colonne d’aria provoca una pressione che tenta di riportarle all’equilibrio. Siccome supponiamo che la pressione venga distribuita istantaneamente dentro tutto il volume, le pressioni alle basi delle colonne d’aria sono identiche. Usando il modulo di compressibilità, la pressione è date da \[\Delta P=-\frac{K}{V}\Delta V=\frac{K}{V}(A_1u_1+A_2u_2)\]
Siccome le sezioni sono diverse, la forza ricevuta dalla colonna 1 è diversa dalla forza ricevuta dalla colonna 2. Le ricaviamo moltiplicando la pressione per la sezione: \[F_1=-\Delta P A_1=-\frac{KA_1}{V}(A_1u_1+A_2u_2)\] \[F_2=-\Delta P A_2=-\frac{KA_2}{V}(A_1u_1+A_2u_2)\]
Il segno negativo viene dal fatto che se la colonna si muove verso il basso, la forza è diretta verso l’alto e viceversa.
Le masse delle colonne d’aria sono \[m_1=\rho A_1L_1\] \[m_2= \rho A_2L_2\]
Scriviamo quindi la legge di Newton per ciascuna delle due masse separatamente:
\[(\rho A_1L_1)\ddot{u}_1=-\frac{KA_1}{V}(A_1u_1+A_2u_2)\]
\[(\rho A_2L_2)\ddot{u}_2=-\frac{KA_2}{V}(A_1u_1+A_2u_2)\]
A questo punto, supponiamo che il moto sia armonico, e che avvenga con la stessa pulsazione \(\omega\) nei due ingressi. In questo caso \(\ddot{u}=-\omega^2u\). Riscrivendo l’equazione in forma di matrice, e moltiplicando per l’inverso della matrice delle masse, abbiamo il seguente sistema:
\[\frac{c^2}{V}\begin{pmatrix}\frac{A_1}{L_1} & \frac{A_2}{L_1}\\ \frac{A_1}{L_2} & \frac{A_2}{L_2}\end{pmatrix}\begin{pmatrix} u_1\\u_2\end{pmatrix} =\omega^2 \begin{pmatrix} u_1\\u_2\end{pmatrix} \]
Le pulsazioni che stiamo cercando sono date da \(\omega^2=(c^2/V)\lambda\), dove \(\lambda\) sono gli autovalori della matrice a sinistra, la cui equazione caratteristica è
\[\lambda \left( \lambda-\frac{A_1}{L_1} -\frac{A_2}{L_2} \right)=0\]
Da cui ricaviamo la soluzione \(\lambda=0\) (equilibrio) oppure la soluzione oscillante \(\lambda=A_1/L_1+A_2/L_2\) con pulsazione naturale (al quadrato):
\[\omega^2=\frac{c^2}{V}\left( \frac{A_1}{L_1} +\frac{A_2}{L_2} \right)\]
Prendendo la radice quadrata e dividendo la pulsazione per \(2\pi\) troviamo la frequenza:
\[f=\frac{c}{2\pi}\sqrt{ \frac{1}{V}\left( \frac{A_1}{L_1} +\frac{A_2}{L_2} \right)}\]
Se la grotta ha più ingressi, ognuno contribuisce con il suo rapporto sezione/lunghezza.
